MHT CET 2019 :: Physics :: General questions

• Physics - General questions

 if $W_{1}$, $W_{2}$ and $W_{3}$ represent the work done in moving a particle from A to B  along three different paths 1,2 and 3 (as shown in fig) in the gravitational field of the point mass 'm'. Find  the correct relation between' $W_{1}$','$W_{2}$' and '$W_{3}$'

Answer:

Explanation:

 Gravitational force is a conservative force. As we know that the work done by a conservative force is independent of the path followed and depends only on the endpoints of the motion. Since in the given pattern $W_{1}$,  $W_{2} $   and $W_{3}$ have  the  same  endpoint A and B as shown  in the figure below,

So, the correct relation between $W_{1}$  =  $W_{2} $   =  $W_{3}$

 Which of the following combinations of 7 identical capacitors each of 2$\mu$ F gives a resultant capacitance of 10/11 $\mu$ F?

Answer:

Explanation:

 Key Idea

       For n capacitors  i.e, C₁, C₂,.......C_n  their equivalent capacitance  , when connected in

  (a) series is given  as,  $\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+....$

and (b) parallel is given as,   $C_{p}=C_{1}+C_{2}+....$

 In the given problem, we will check the net capacitance in each option and compare it with the desired capacitance mentioned in it.

   (a)   3 capacitors are in parallel and 4 capapcitors are connected in series, i.e,

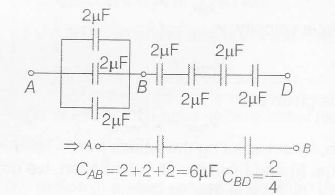
 where, C_AB is the equivalent capacitance  of parallel branches between A and C and  C_BD is equivalent capacitance of series capacitors  between B and D , So , equivalent capacitance

$C_{eq}=\frac{C_{AB}.C_{BD}}{C_{AB}+C_{BD}}=\frac{6\times\frac{2}{4}}{6 +\frac{2}{4}}=\frac{6}{13}\mu F$

 Similarly,

 (b) 2 capacitors are in parallel and 5 capacitors are connect in series i.e,

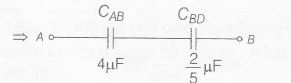
 So, equivalent capacitance,

  $C_{eq}==\frac{4\times\frac{2}{5}}{4 +\frac{2}{5}}=\frac{4}{11}\mu F$

 (c)   4 capacitors are in parallel and 3 capacitors are connect in series  i.e,

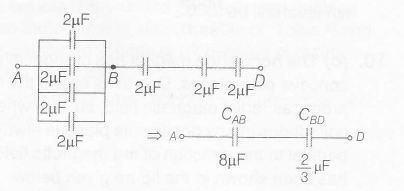
 So, equivalent capacitance,

$C_{eq}=\frac{8\times\frac{2}{3}}{8 +\frac{2}{3}}=\frac{16}{26}=\frac{8}{13}\mu F$

 (d)    5 capacitors are in parallel and 2 capacitors are connect in series i.e,

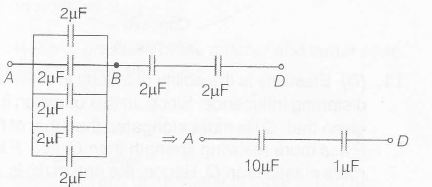
 So, equivalent capacitance

$C_{eq}=\frac{10\times1}{10 +1}==\frac{10}{11}\mu F$

 So, the correct option is (d) 

 If 'C_p' and 'C_v' are molar specific heats of an ideal gas at constant pressure and volume respectively, I f ' $\lambda$ ' is the ratio of two specific heats and ' R'  is universal gas constant then 'C_p' is equal to

Answer:

Explanation:

 Given, that   $\frac{C_{p}}{C_{V}}=\gamma$...........(i)

 as we know that from Mayer's relation  C_p- C_V= R

 where R= universal gas constant

 Substitute  the valUe of C_p from the above relation  in Eq.(i) , we get

 $\gamma=\frac{C_{V}}{C_{p}-R}$

 $\gamma(C_{p}-R)=C_{p}$

$\Rightarrow$     $\gamma C_{p}-C_{p}=\gamma R$

   $C_{p}(\gamma-1)=\gamma R$

 $\Rightarrow C_{p}=\frac{\gamma R}{\gamma-1}$

 Hence, C_p  is equal to  $\frac{\gamma R}{\gamma-1}$

Two coils have a mutual inductance of 0.01 H. The current in the first coil changes according to equation, l=5sin 200$\pi$t. The maximum value of emf induced in the second coil is 

Answer:

Explanation:

 Given, mutual inductance in the coil, M=0.01 H and current in coil, l=5 sin 200 $\pi$t

 emf induced in secondary coil is given,

$e=M\frac{dl}{dt}$

 putting the value in the above relation,

$e=0.01\frac{d}{dt}(5\sin 200\pi t)$

   $=0.01 \times 5\times200\pi \cos 200 \pi t=10\pi\cos 200\pi t$

 Compairing the above equation with the general equation  of induced emf, which is represented as,

 $e=e_{0}\cos \omega t$

 where, e₀ is the maximum value of the emf.

$\therefore$  In the question , the maximum value of emf induced in the coil is ;   $e_{0}=10\pi V$

• Physics - General questions